طرح درس روزانه ریاضی هفتم مبحث معادله

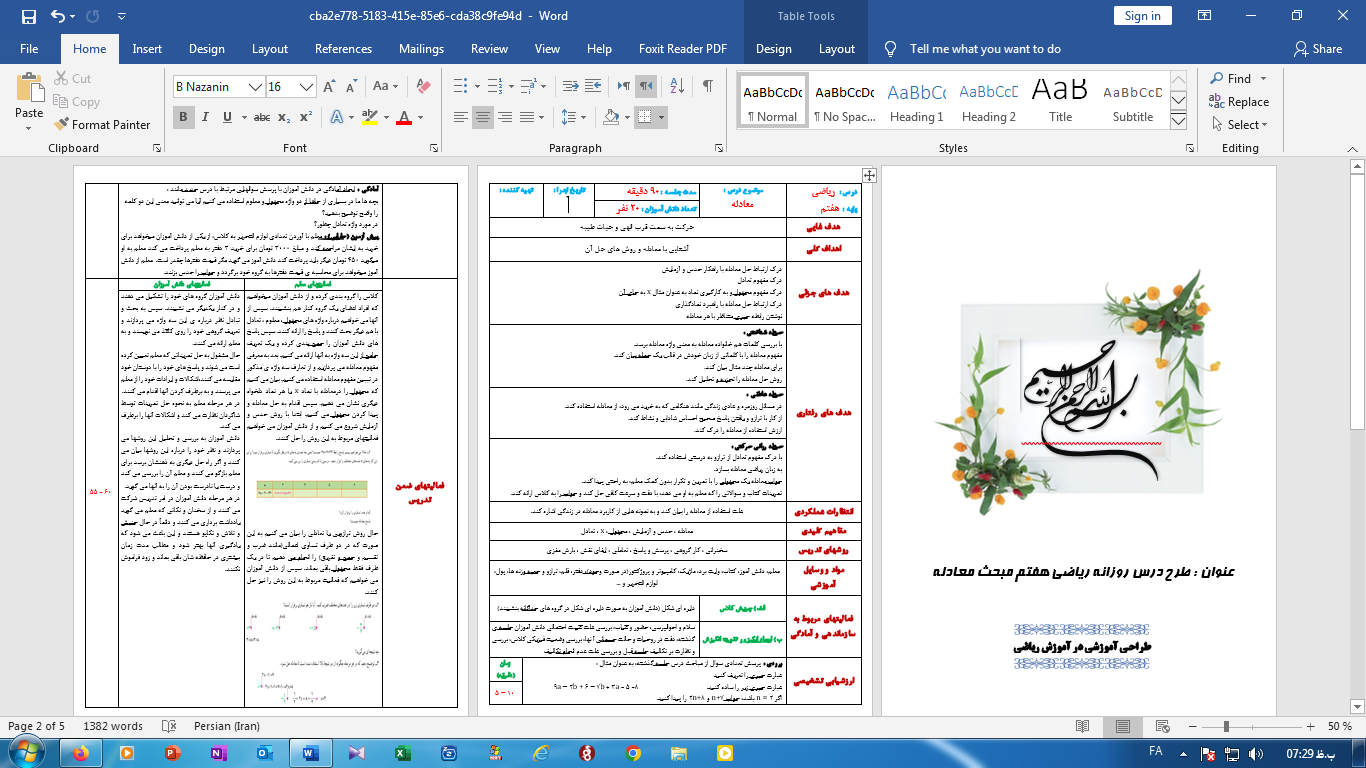
دانلود طراحی آموزشیپیشرفته از درس ریاضی هفتم مبحث معادله. طراحی شده به عنوان تکلیف برای درس طراحی آموزشی در آموزش ریاضی در قالب word و در 5 صفحه تهیه و تنظیم شده است

یادگیری مبحث معادله در ریاضی پایه هفتم از جمله بخش‌های کلیدی آموزش این پایه است که زمینه‌ساز حل مسائل پیچیده‌تر در پایه‌های بالاتر می‌باشد. معادله نه تنها یک ابزار ریاضی است، بلکه روشی برای مدل‌سازی مسائل دنیای واقعی و توسعه تفکر منطقی و استدلالی دانش‌آموزان است. آشنایی دانش‌آموزان با مفهوم معادله، متغیر (مجهول)، تساوی و روش‌های پیدا کردن مقدار مجهول، به پرورش تفکر تحلیلی و منطقی آنها کمک می‌کند. در این طرح درس روزانه، با رویکرد فعالیت‌محور و مشارکت گروهی، معادله به صورت عینی و ملموس آموزش داده می‌شود تا یادگیری پایدار شکل گیرد و دانش‌آموزان صرفاً با حفظ کردن روش، بلکه با درک اصل «تعادل» به حل مسئله بپردازند.

🔹 اطلاعات کلی طرح درس

عنوانجزئیاتپایههفتم متوسطه اولدرسریاضیموضوع اصلیمعادله (معادلات تک‌مجهولی خطی)زمان تدریس۴۵ دقیقه (یک زنگ)هدف کلیآشنایی با تعریف معادله، درک مفهوم تعادل ریاضی و توانایی یافتن مقدار مجهول در معادلات ساده تک‌مجهولی با یک مرحله عملیات اصلی (جمع/تفریق)وسایل کمک آموزشیتخته هوشمند/وایت‌برد، ماژیک‌های رنگی، کارت‌های اعدادی یا نمادین برای نمایش مجهول، ترازو دو کفه یا تصویر گرافیکی دقیق از ترازو (به عنوان مدل اصلی)، دفتر ریاضی دانش‌آموزان، برگه‌های کار گروهی.

🔹 اهداف رفتاری

پس از اتمام جلسه، انتظار می‌رود دانش‌آموزان در سه حوزه زیر به اهداف مشخصی دست یابند:

۱. حوزه دانش (Cognitive Domain)

تعریف معادله: دانش‌آموز بتواند معادله را به عنوان یک جمله‌ی تساوی که حداقل یک عبارت نامعلوم (مجهول) دارد، تعریف کند.

شناسایی اجزا: دانش‌آموز بتواند اجزای یک معادله (طرف چپ، طرف راست، علامت مساوی، مجهول) را نام ببرد و مشخص کند.

۲. حوزه مهارت (Psychomotor Domain)

حل با تعادل: دانش‌آموز بتواند معادلات ساده تک‌مجهولی شامل جمع و تفریق عددی (مانند (x + a = b) یا (x - a = b)) را با استفاده از اصل حفظ تعادل (انجام عمل قرینه در دو طرف) به درستی حل کند.

تبدیل کلامی به جبری: دانش‌آموز بتواند یک مسئله ساده کلامی را به صورت یک معادله جبری بنویسد.

۳. حوزه نگرش (Affective Domain)

علاقه‌مندی به مدل‌سازی: دانش‌آموز به استفاده از مدل عینی (ترازو) برای فهم عمیق‌تر مفاهیم انتزاعی معادله علاقه‌مند شود.

ارزش‌گذاری کار گروهی: دانش‌آموز درک کند که حل مسائل ریاضی نیازمند همکاری و تبادل نظر با همکلاسی‌ها است.

دقت در مراحل: دانش‌آموز به لزوم انجام دقیق مراحل حل برای رسیدن به پاسخ صحیح و حفظ تساوی اهمیت دهد.

🔹 مراحل تدریس (روش فعال یاددهی–یادگیری)

مدت زمان کل: ۴۵ دقیقه

۱. مرحله آماده‌سازی و ایجاد انگیزه (۵ دقیقه)

فعالیت: نمایش اصل تساوی با ترازو

معلم با استفاده از یک تصویر بزرگ از یک ترازوی دو کفه (یا یک ترازوی فیزیکی اگر موجود باشد) شروع می‌کند.

ترازو را در حالت تعادل نشان می‌دهد. روی کفه چپ ۵ واحد وزن (مثلاً سنگ یا کارت عدد ۵) و روی کفه راست ۵ واحد وزن قرار می‌دهد.

پرسش محرک: «بچه‌ها، الان ترازو در چه وضعیتی است؟» (پاسخ مورد انتظار: متعادل/تساوی)

معلم روی کفه چپ ۲ واحد اضافه می‌کند. «حالا چه اتفاقی افتاده؟» (کفه سنگین شده است).

پرسش کلیدی: «برای اینکه دوباره ترازو به تعادل برسد، چه کاری باید انجام دهیم؟» (پاسخ‌های احتمالی: ۲ واحد کم کنیم، ۲ واحد اضافه کنیم و...)

معلم تاکید می‌کند که «برای حفظ تساوی، باید عملی را که در یک طرف انجام می‌دهیم، عیناً در طرف دیگر نیز انجام دهیم.»

ارتباط با ریاضی: معلم بیان می‌کند که امروز قرار است همین مفهوم تعادل را برای حل مسائل ریاضی که در آن‌ها عددی مجهول است، به کار ببریم. این مجهول همان «کفه نامعلوم» ترازو است.

۲. مرحله ارائه و توضیح درس (۲۰ دقیقه)

فعالیت: معرفی معادله و حل نمونه

تعریف واژگان (۵ دقیقه):

معلم واژه «معادله» را معرفی می‌کند: «معادله، جمله‌ای ریاضی است که نشان‌دهنده تساوی بین دو عبارت است و حداقل یک نماد مجهول دارد.»

تعریف مجهول (Variable): نمادی که مقدار آن نامعلوم است (معمولاً (x)).

نوشتن روی تخته: [ \text{طرف چپ} = \text{طرف راست} ] مثال: (x + 3 = 7)

مدل‌سازی با ترازو (۱۰ دقیقه):

معلم معادله (x + 3 = 7) را روی تخته می‌نویسد و همزمان آن را با ترازو مدل‌سازی می‌کند:

کفه چپ: یک شیء نمادین برای (x) (مثلاً یک جعبه یا کارت آبی) + ۳ کارت عدد.

کفه راست: ۷ کارت عدد.

هدف: پیدا کردن مقدار (x) یعنی پیدا کردن عددی است که داخل آن جعبه قرار گیرد تا ترازو متعادل بماند.

روش حل: برای تنها کردن (x)، باید عدد ۳ را از کفه چپ حذف کنیم (عمل قرینه: تفریق ۳).

بر اساس اصل تعادل، معلم حتماً عدد ۳ را از کفه راست هم کم می‌کند: [ x + 3 - 3 = 7 - 3 ] [ x + 0 = 4 ] [ x = 4 ]

معلم تأکید می‌کند: «علامت جمع (+) در یک طرف، با تفریق (-) در طرف دیگر جبران می‌شود تا مجهول تنها بماند.»

حل نمونه دوم (۵ دقیقه):

معادله‌ای با تفریق ارائه می‌شود: (x - 2 = 10)

مدل‌سازی با ترازو (کفه چپ: جعبه و ۲ واحد کسر شده، کفه راست: ۱۰ واحد).

برای خنثی کردن تفریق ۲، باید ۲ واحد اضافه کنیم (جمع ۲): [ x - 2 + 2 = 10 + 2 ] [ x = 12 ]

۳. مرحله فعالیت گروهی و تمرین (۱۰ دقیقه)

فعالیت: بازی "تعادل‌یاب‌ها"

کلاس به ۴ یا ۵ گروه تقسیم می‌شود.

به هر گروه یک برگه‌ی کار داده می‌شود که شامل سه معادله در سطوح زیر است:

گروه ۱: (x + 5 = 11)

گروه ۲: (x - 4 = 8)

گروه ۳: (x + 1 = 6)

گروه ۴: (x - 7 = 3)

از هر گروه خواسته می‌شود که مراحل حل را به صورت کامل (نوشتن معادله، انجام عملیات در دو طرف، و پاسخ نهایی) روی یک برگه بزرگ نوشته و به صورت شفاهی، دلیل انجام آن عملیات را توضیح دهند (مثلاً: «ما برای تنها کردن (x)، عدد ۵ را از هر دو طرف کم کردیم»).

معلم در حین فعالیت در گروه‌ها چرخش می‌کند و به رفع اشکال می‌پردازد.

۴. مرحله جمع‌بندی و ارزشیابی پایانی (۱۰ دقیقه)

الف) جمع‌بندی (۵ دقیقه):

معلم به صورت سریع، مهم‌ترین نکات را مرور می‌کند:

معادله یعنی تساوی.

هدف ما تنها کردن مجهول ((x)) است.

کلید حل معادله: اصل تعادل (هر عملی در یک طرف، باید در طرف دیگر هم انجام شود).

برای حذف یک عدد، باید عمل قرینه آن را در دو طرف انجام دهیم (مثلاً حذف (+5) با (-5)).

ب) ارزشیابی پایانی سریع (۵ دقیقه):

معلم ۳ پرسش شفاهی و کوتاه مطرح می‌کند و پاسخ‌های صحیح را در دفتر دانش‌آموزان بررسی می‌کند:

پرسش دانش: اگر معادله‌ای نداشته باشد، به آن چه می‌گوییم؟ (جمله‌ی تساوی یا اتحاد، اما معادله نیست)

پرسش مهارت: مقدار (x) در معادله (x + 15 = 20) چند است؟ (پاسخ: ۵)

پرسش نگرش: چرا باید در هر دو طرف معادله یک عمل مشابه انجام دهیم؟ (برای حفظ توازن و تساوی)

تکلیف منزل:
حل ۵ معادله یک‌مرحله‌ای مشابه از تمرین‌های کتاب درسی (تمرکز بر جمع و تفریق).

🔹 ارزشیابی تفصیلی

زمان ارزشیابیابزار سنجشمعیار سنجشحین تدریس (مرحله ۲ و ۳)مشاهده مستقیم عملکرد گروهی و پاسخ‌های شفاهیتوانایی دانش‌آموز در درک مدل ترازویی و درخواست عملیات صحیح برای تنها کردن مجهول.پایان تدریس (مرحله ۴)پرسش شفاهی و مرور پاسخ‌های گروهی روی تختهسنجش میزان درونی‌سازی تعریف معادله و روش حل پایه‌ای.پس از تدریس (تکلیف منزل)بررسی دفتر تمرین در جلسه بعدتثبیت مهارت حل عملیات جمع و تفریق در دو طرف معادله.

🔹 نکات تکمیلی و ملاحظات اجرایی

بصری‌سازی قوی: استفاده مداوم از ماژیک‌های رنگی برای تفکیک طرف چپ و راست و همچنین استفاده از نماد بصری برای عملیات قرینه (مثلاً کشیدن یک خط بین دو طرف معادله و نوشتن عملیات در زیر آن خط).

تمایز سطح‌بندی:

دانش‌آموزان ضعیف‌تر: استفاده از اعداد کوچک‌تر (مانند اعداد تک‌رقمی) و تمرین دادن با مدل فیزیکی ترازو به صورت انفرادی.

دانش‌آموزان تیزهوش: در صورت اتمام سریع تکالیف، یک معادله‌ی دو مرحله‌ای ساده مانند (2x - 1 = 7) یا معادلات شامل کسر واحد ((x + \frac{1}{2} = 2)) به عنوان چالش مطرح شود.

تأکید بر تبدیل: در صورت وجود وقت، یک مسئله کلامی ساده (مثلاً: عددی که ۵ واحد از آن کم کنیم، می‌شود ۹. آن عدد چیست؟) به دانش‌آموزان داده شود تا مهارت تبدیل متن به نماد جبری تقویت شود.

🔹 جمع‌بندی نهایی و نتیجه‌گیری

در پایان این جلسه، دانش‌آموزان باید قادر باشند با استفاده از روش تعادل، معادلات ساده‌ی یک‌مرحله‌ای را شناسایی و حل کنند. آموزش گام‌به‌گام همراه با مشارکت گروهی، علاوه بر درک مفاهیم، موجب علاقه‌مندی به ریاضی به عنوان یک ابزار منطقی خواهد شد. تمرکز بر مدل‌سازی عینی (ترازو) به دانش‌آموز کمک می‌کند تا ماهیت حفظ تساوی را به جای حفظ صرف فرمول، یاد بگیرد.

این طرح درس در قالب فایل ورد قابل ویرایش و مناسب برای دبیران ریاضی پایه هفتم طراحی شده است تا امکان انعطاف‌پذیری بر اساس شرایط کلاس فراهم باشد.

📘 تهیه و تنظیم: پارسا – معاون اجرایی مدارس استعدادهای درخشان
💻 انتشار ویژه در: PDF Doc
📞 ارتباط: @drsifile | @pdfdocir | ✉️ drsifile@yahoo.com

کلمات کلیدی: طرح درس روزانه ریاضی هفتم, مبحث معادله, فایل ورد طرح درس ریاضی پایه هفتم, طرح درس آماده معادله, آموزش معادله در پایه هفتم, دانلود طرح درس ریاضی متوسطه اول, طرح درس سئو شده پارسا, حل معادله با ترازو, معادله تک مجهولی هفتم.